Способы оценки рисков

± Ес >= 0;

± Ет >= 0; Ś = (1, 1, 1) (8)

± Ен >= 0;

Нормальная устойчивость финансового состояния задается условиями:

± Ес ≈ 0;

± Ет ≈ 0; Ś = (1, 1, 1) (9)

± Ен ≈ 0;

Неустойчивое финансовое состояние предприятия задается условиями:

± Ес < 0;

± Ет >= 0; Ś = (0, 1, 1) (10)

± Ен >= 0;

Критическое финансовое состояние задается условиями:

± Ес < 0;

± Ет < 0; Ś = (0, 0, 1) (11)

± Ен >= 0;

Кризисное финансовое состояние задается условиями:

± Ес < 0;

± Ет < 0; Ś = (0, 0, 0) (12)

± Ен < 0;

На рисунке 1.5. поясняется экономический смысл классификации финансовых ситуаций в зависимости от основных областей риска. При этом ± Ес ≈ ± Еа.

Из таблицы видно, что анализ абсолютных показателей устойчивости, который включает в себя исследование состояния запасов и затрат, равен возможным потерям в области риска.

Для принятия правильных решений нужны реальные количественные характеристики надежности и риска, а не их имитация. Они обязательно должны иметь понятное содержание. Такими характеристиками могут быть только вероятности.

При принятии решений могут быть использованы как объективная, так и субъективная вероятности. Первую можно рассчитать на основе показателей бухгалтерской и статистической отчетности.

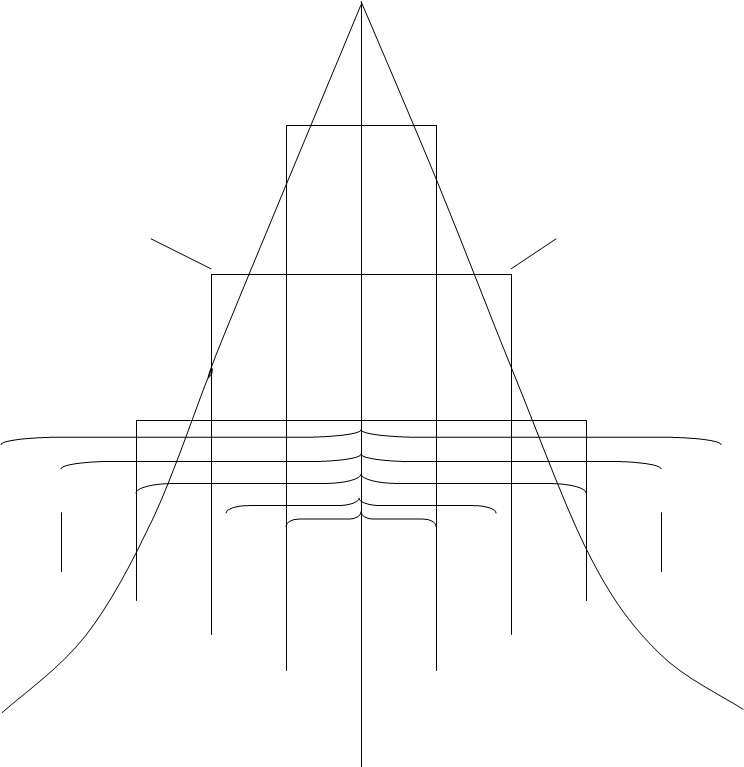0,75

Кривая

финансового

состояния Кривая

0,5 риска

0,25

I.

II.

III.

IV.

V.

Еа Ес Ет Ен 0 Г1 В1 Б1 А1

Области финансового состояния Возможные потери в областях риска

Рис. 2. Построение кривой риска и финансового состояния фирмы в зависимости от возможных потерь и степени устойчивости финансов.

Лемма Маркова гласит [14]: если случайная величина Х не принимает отрицательных значений, то для любого положительного числа α справедливо следующее неравенство:

Р (Х > α) ≤ М (х) / α, (13)

где М (х) – математическое ожидание, то есть среднее значение случайной величины;

Х – любая случайная величина.

Неравенство Чебышева имеет вид:

Р(|х - х| > ε) ≤ σ²/ε². (14)

Оно позволяет находить верхнюю границу вероятности того, что случайная величина Х отклонится в обе стороны от своего среднего значения на величину больше ε.

Эта вероятность равна или меньше (как максимум равна, не больше), чем σ²/ε², где σ² - дисперсия, исчисляемая по формуле:

σ² = Σ (х – х)² / n. (15)

Если нас интересует вероятность отклонения только в одну сторону, например, в большую, то вышеприведенное неравенство Чебышева надо было бы записать так:

Р ((х – х) > ε) ≤ σ² / (ε²*2). (16)

Неравенство Чебышева дает значение вероятности отличное от значения, полученного решая лемму Маркова. Это объясняется тем, что неравенство Чебышева кроме среднего уровня показателей учитывает и еще его колеблемость.

Это интересно:

Тарифы страховых взносов
Тарифы страховых взносов с 1 января 2011 года: Пенсионный фонд Фонд социального страхования Фонды обязательного медицинского страхования Итого Федеральный Территориальный 26% 2,9% 3,1% 2% 34% Пониженные тарифы с 1 января 2011 года: Пенсионный фонд Фонд социального страхования Фонды обязательного ме ...

Определение налогооблагаемого оборота
Налог на добавленную стоимость представляет собой форму изъятия в бюджет части добавочной стоимости, создаваемой на всех стадиях производства. Он определяется как разница между стоимостью реализованных товаров, работ и услуг и стоимостью материальных затрат, отнесенных на издержки производства и об ...

Единый налог на вмененный доход для отдельных видов деятельности
Система налогообложения в виде единого налога на вмененный доход (ЕНВД) регулируется гл. 26 НК РФ и применяется по решениям представительных органов муниципальных районов, городских округов, законодательных органов государственной власти городов федерального значения Москвы и Санкт - Петербурга. Вм ...