Аналитические методы оценки эффективности фискальной политики

Подобная схема расчетов основана на конструировании системы уравнений (4), (6) и (7) и ее решении относительно параметров a , b и g , что позволяет охарактеризовать эту схему как аналитическую или алгебраическую. Решение системы (4), (6), (7) дает следующие формулы для оцениваемых параметров:

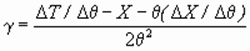, (8)

, (9)

. (10)

Идентификация параметров функций (4) и (5) позволяет элементарно определить точки Лаффера. При этом точка Лаффера первого рода q*, когда dX/dq =0, определяется по формуле

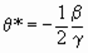, (11)

а точка Лаффера второго рода q**, когда d2T/dq 2=0, находится в результате решения следующего квадратного уравнения

(12)

и в итоге вычисляется по формуле

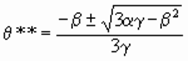. (13)

Дополнительное исследование свойств функций (4) и (5) позволит определить, являются ли найденные стационарные точки точками Лаффера. Если стационарные точки окажутся точками локального минимума или их значения выйдут за область допустимых значений, то точки Лаффера отсутствуют.

Альтернативой рассмотренному трехпараметрическому методу может служить подход, базирующийся на использовании в качестве производственной функции усеченного полинома третьей степени:[15]

.

При этом число параметров не меняется, оставаясь равным трем. В этом случае процедура отыскания лафферовых точек корректируется с учетом исходной кубической зависимости, а стационарные точки для фискальной кривой будут отыскиваться в результате решения кубического уравнения. Понятно, что такой алгоритм может генерировать две точки Лаффера второго рода. На наш взгляд, в силу большей однозначности и наглядности на практике следует использовать первый, базовый вариант трехпараметрического метода.

Следует отметить, что аналитический метод оценки эффективности фискальной политики позволяет использовать функциональные зависимости с числом параметров, не превышающим трех. Большее число параметров требует добавления к базовой системе (4), (6), (7) дополнительных уравнений, что невозможно из-за узкой постановки исходной задачи.

2. Двухпараметрический метод. В основе данного метода лежит аппроксимация процесса экономического роста усеченной квадратичной функцией, включающей только два параметра:

. (14)

Тогда сумма фискальных поступлений равна

. (15)

Дополнительное ограничение, накладываемое на функциональные свойства производственной системы, задается уравнением, аналогичным (6):

. (16)

Построенная система уравнений (14), (16) достаточна для отыскания параметров b и g . Как и в случае использования трехпараметрического метода, уравнение (14) воспроизводит “точечные” свойства производственной системы, а уравнение (16) – “интервальные”. При этом вспомогательное уравнение, задающее динамические свойства фискальной системы, отсутствует; по умолчании считается, что получаемая сумма налогов полностью детерминируется активностью производственной системы и уровнем фискального давления.

Это интересно:

Методика оценки и анализ финансового состояния предприятия
Метод экономического анализа представляет собой способ подхода к изучению хозяйственных процессов в их плавном развитии. Характерными особенностями метода экономического анализа являются: определение системы показателей, всесторонне характеризующих хозяйственную деятельность организаций; установлен ...

Анализ финансовой устойчивости
Данные для расчета финансовой устойчивости организации взяты из формы №1 «Бухгалтерский баланс». Рассчитаем следующие показатели за отчетный и предыдущий периоды: 1) СОСот = 2 946 015 721 – 3 238 888 447 = - 292 872 726, (7) СОС пред = 2 971 891 963 – 3 470 252 441 = - 498 360 478. (7) Наличие собс ...

Угрозы экономической безопасности Ставропольского края
Прежде чем приступить к рассмотрению угроз, которые присутствуют в экономике Ставрополья, а также тех, которые могут появиться, необходимо обозначить угрозы безопасности всей Российской Федерации, т. к. они автоматически влияют на состояние экономики любого региона федерации, в частности, Ставропол ...