Эффективность фискальной политики государства

В последнее время проводится много исследований, в которых делается попытка оценить эффективность отдельных сторон фискальной системы с помощью отыскания точек Лаффера для конкретных видов налоговых сборов. [9]

Вместе с тем концепция кривой Лаффера изначально создавалась применительно к понятию совокупного налогового бремени, т. е. всей массы налоговых отчислений. Далее придерживаемся именно такого понимания проблемы и, следовательно, будем отыскивать точки Лаффера для усредненного макроэкономического показателя налогового бремени. Под последним мы будем понимать долю налоговых поступлений в консолидированный бюджет страны в объеме валового внутреннего продукта (ВВП).

В основе нашего исследования лежит предположение, что объем производства Х, отражаемый величиной ВВП, зависит от уровня налогового бремени q =T/X, где T – сумма налоговых поступлений в бюджет страны.[10] Зависимость X(q) аппроксимируется нелинейной функцией, параметры которой подлежат количественной оценке. Идентификация функции X(q) позволит рассчитать точки Лаффера. При этом нами будут различаться точки Лаффера первого и второго рода. Дадим соответствующие определения.

Точкой Лаффера первого рода будем называть такую точку q*, при которой производственная кривая X=X(q) достигает локального максимума, т. е. когда выполнены условия: dX(q*)/dq =0; d2X(q*)/dq 2<0.[11] Точкой Лаффера второго рода будем называть такую точку q**, при которой фискальная кривая T=T(q) достигает локального максимума, т. е. когда выполнены условия: dT(q**)/dq =0; d2T(q**)/dq 2<0. Экономически точка Лаффера первого рода означает тот предел налогового бремени, при котором производственная система не переходит в режим рецессии. Точка Лаффера второго рода показывает величину налогового бремени, за пределами которой увеличение массы налоговых поступлений становится невозможным.

Идентификация двух точек Лаффера и их сопоставление с фактическим налоговым бременем позволяет оценить эффективность налоговой системы страны и направления ее оптимизации.[12] Рассмотрим некоторые подходы, с помощью которых поставленная задача может быть решена.

В общем случае поставленную задачу можно решить эконометрическими способами, в основе которых лежит постулат о том, что объем производства нелинейно зависит от величины налогового бремени. В этом случае объем ВВП достаточно аппроксимировать полиномиальной регрессией следующего вида:

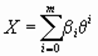, (1)

где b i – параметры, подлежащие статистической оценке на основе ретроспективных динамических рядов.

Учитывая формулу (1) и величину массы налогов:[13]

, (2)

можно записать следующее соотношение:

(3)

Для проведения соответствующих расчетов весь информационный массив должен быть представлен динамическими рядами двух “первичных” показателей – X и T. Зная эти величины, по формуле (2) можно рассчитать ретроспективный ряд для такого “вторичного” показателя, как q. В дальнейшем в результате вычислительных экспериментов отыскивается полином (1) соответствующей степени. Желательно, чтобы это была квадратичная или, в крайнем случае, кубическая функция, так как более высокий порядок полинома впоследствии осложнит отыскание точек Лаффера.

Учитывая специфику операций сглаживания рядов, эконометрические модели типа (1) имеют ряд очевидных особенностей. Во-первых, для получения значений параметров b i необходимо иметь достаточно длинные и “хорошие” в статистическом смысле динамические ряды. Во-вторых, параметры b i постоянны во времени, что в некоторых случаях приводит к неизменности значений точек Лаффера. Это не совсем правомерно, так как более логично было бы предположить, что точки Лаффера являются “плавающими” во времени величинами.

Комментируя предлагаемый выше подход, который базируется на примитивной полиномиальной аппроксимации процесса экономического роста налоговой функцией (1), следует сразу оговориться: в данном случае решается чисто техническая, инструментальная проблема без учета внутрисистемных экономических связей. Явного моделирования функциональных свойств системы не ведется, однако они косвенно улавливаются зависимостью (1). При этом, хотя сама функциональная зависимость (1) нелинейна, регрессия (1), наоборот, линейна относительно входящих в нее параметров и, следовательно, никаких особых технических сложностей при ее идентификации не возникает. В этом состоит один из существенных плюсов предлагаемой модельной схемы.

Это интересно:

Заемные источники финансирования прямых инвестиций
К заемным денежным средствам относятся долгосрочные кредиты банков, которые могут предоставляться предприятиям: ▪ на строительство, расширение, реконструкцию и техническое перевооружение объектов производственного и непроизводственного назначения; ▪ на приобретение недвижимого имущества ...

Налогообложение прибыли предприятий
Налог на прибыль предприятий - это основной прямой налог, взимаемый с юридических лиц в Украине. Он обеспечивает значительные поступления в бюджетную систему. Налогообложение прибыли (дохода) предприятий постоянно находится в центре внимания законодателей, которые неоднократно принимали попытки усо ...

Вывод
Субъекты малого предпринимательства при осуществлении хозяйственной деятельности могут применять общую систему налогообложения либо специальные налоговые режимы (упрощенную систему налогообложения и единый налог на вмененный доход). Первое, что интересует руководителей при выборе системы налогообло ...